下面记录一下二叉树的一些简单常用理论。

一、种类

1. 满二叉树

• 节点数量：2^k - 1（k 是深度，从头 1 开始）

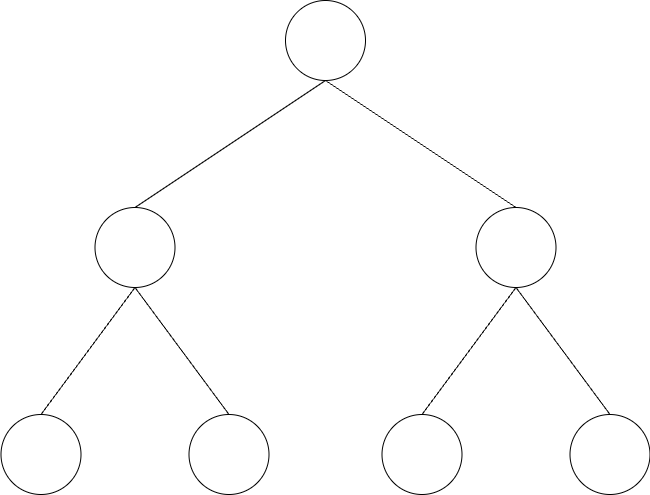
2. 完全二叉树

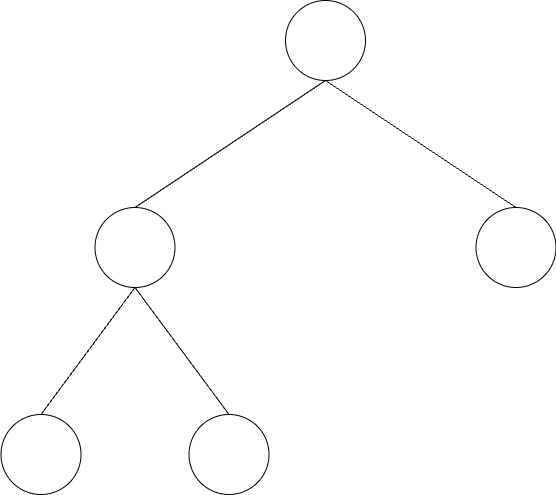
除了底层以外，其他层都是满的。底层不一定满，节点从左到右连续。

满二叉树一定是完全二叉树。

堆其实就是完全二叉树。

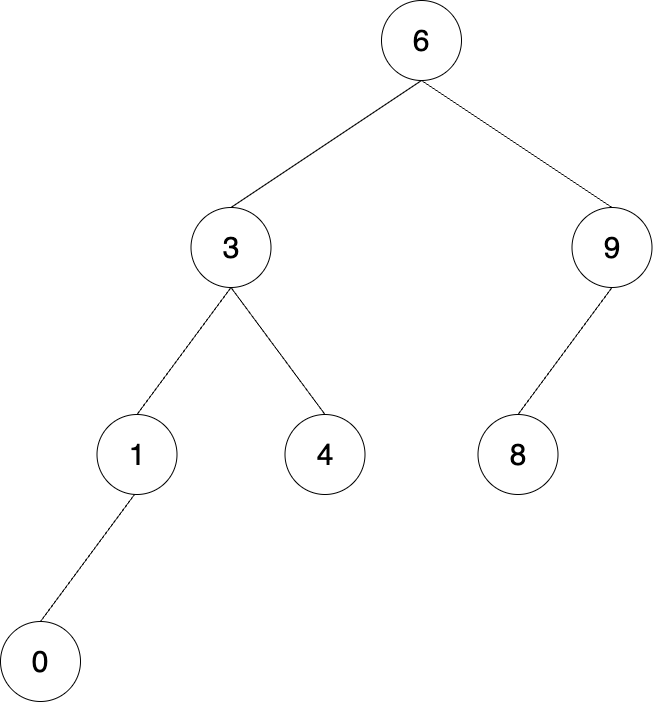
3. 二叉搜索树

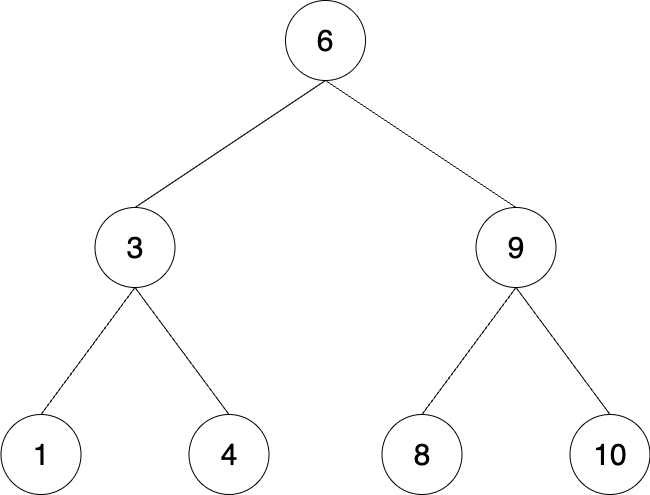
对节点结构没有要求，但是对节点上的元素有顺序要求。

左子树所有节点都小于中间节点，右子树所有节点都大于中间节点。

查询时间复杂度：O(logn)。

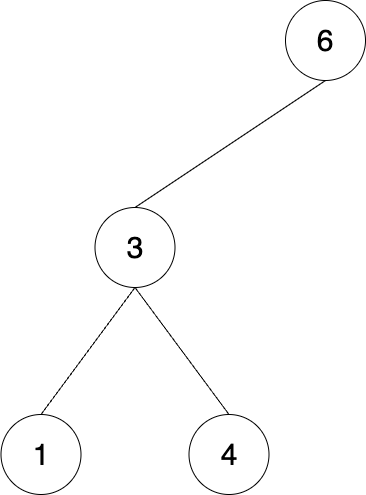
4. 平衡二叉树搜索树

平衡二叉树：每个节点的左右子树高度差不能超过 1。

C++ 中的 map, set, multimap，multiset 底层实现都是平衡二叉搜索树（元素有序）。

插入和查询的时间复杂度都是 O(logn)。

二、存储方式

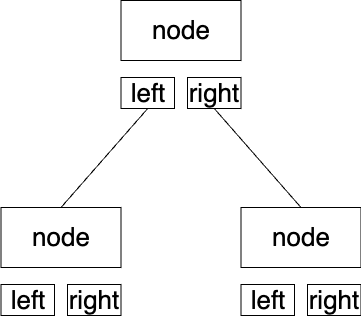
1. 链式存储

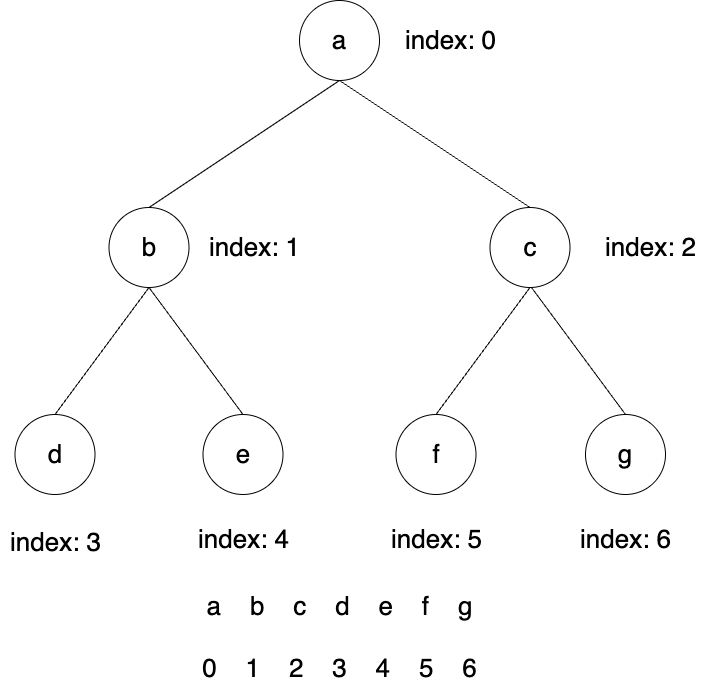
2. 线性存储

完全二叉树存储。

假定一个元素索引为 i：

• 左孩子节点：2 * i + 1
• 右孩子节点：2 * i + 2

三、遍历方式

1. 深度优先搜索 (DFS)

一般通过 递归 实现，也可以使用迭代法遍历。

前中后序遍历都是通过深度优先搜索来实现。

一个方向一直搜索到终点，然后再回退换另一个方向继续搜索到终点。

• 前序遍历：中左右
• 中序遍历：左中右
• 后序遍历：左右中

2. 广度优先搜索 (BFS)

一层一层的遍历，层序遍历 就是广度优先搜索的一种。

层序遍历 使用队列来实现对二叉树一层一层的搜索。

四、二叉树定义

// Kotlin
data class TreeNode<T> (
	var value: T,
  var left: TreeNode<T>,
  var right: TreeNode<T>
)

// Swift
class TreeNode<T> {
  var val: T
  var left: TreeNode<T>
  var right: TreeNode<T>
    
    init(val: T, left: TreeNode<T>, right: TreeNode<T>) {
        self.val = val
        self.left = left
        self.right = right
    }
}